Blog

Los orígenes no tan rioplatenses del juego

El truco es probablemente el juego de cartas más icónico en Uruguay. Si bien siempre se asocia con la cultura gauchesca, para encontrar su origen hay que remontarse varios siglos atrás, y a varios miles de kilómetros del Río de la Plata, pues se estima que su origen fue en el siglo XV, y fueron los árabes sus creadores. Luego fueron los españoles los que adoptaron el juego, para luego llevarlo a puertos de lo que era el virreinato del Río de la Plata. En principio lo adoptó la gente del campo, pero luego fue extendiéndose dentro de las ciudades, para luego convertirse en un clásico de los bares y pulperías.

De sur a norte y de oriente a occidente

Tras ver el largo camino del truco, desde sus orígenes hasta nuestras tierras, no nos debería sorprender que el juego de cartas se juegue en otros muchos países. Así es que no solo en Uruguay o Argentina se juega, sino que el juego también fue adoptado por pobladores de otros países latinoamericanos, como Venezuela o Paraguay. Incluso cruzado el charco, en zonas de España o Italia, se puede encontrar el juego entre los saberes populares. Si bien el truco es conocido y jugado en los más diversos rincones del mundo, cada país ha desarrollado su propia versión, adaptando, modificando o incluso agregando algunas reglas.

Entre el azar y el engaño

La principal complejidad del truco, a nivel mundial, reside en la necesidad de tener que engañar al rival y evitar ser engañado por el mismo. Sin embargo, el truco uruguayo presenta ciertas variaciones, principalmente el uso de una Muestra, que hacen que tenga una complejidad y dinamismo superior a las variaciones jugadas en otros países, a la vez que aumenta la influencia del azar en el juego. Así que si bien el Truco no es uruguayo de por si, lo que sí lo es es la forma que tenemos acá de jugarlo.

La no viabilidad de hacer números

La mayoría de los uruguayo alguna vez jugó al truco, alguna vez cantó una flor y alguna que otra vez perdió un envido con 36, sin embargo, casi nadie sabe qué probabilidad hay detrás de estos eventos, que nos pueden dar las mayores alegrías o las peores amarguras. Alguien que esté empezando a estudiar probabilidad y estadística, armado de sus técnicas de conteo y combinatoria, podría aventurarse a intentar calcular estas probabilidades, que desfilan en cada baraje, invisibles a la mayoría de los ojos. Sin embargo, rápidamente se dará cuenta que esta tarea, si bien posible, es demasiado ardua y propensa al error, sobre todo cuando preguntamos cosas más específicas.

Juguemos, millones de veces

Es acá donde entra el enfoque que abordaremos en este blog. Este enfoque consiste en, utilizando una computadora, simular millones o incluso billones de manos de una partida de truco. De esta manera, si quiero saber cual es la probabilidad de tener flor, simplemente tengo que ver en cuantas manos hubo flor, y comprarla con la cantidad total de manos que simule, y así con cualquier otra pregunta que nos hagamos. Simplemente tenemos que programar las simulaciones, y luego contar lo que queramos. El único detalle, es que lo que voy a obtener son aproximaciones de estas probabilidades, si quiero que las aproximaciones sean buenas, tengo que tomar suficientes simulaciones como para cubrir la rareza de lo que estoy contando.

¿Es un evento raro tener flor?

Echa ya la introducción, vamos a empezar a responder preguntas que todos alguna vez (capaz) nos hicimos. En primer lugar veamos que tan probable es tener una flor en una mano cualquiera. Entonces, la chance de tener flor es…15.46%.

¿Cuántas piezas deberá esperar?

Otra cosa que podemos ver, es qué tan probable es tener una pieza, o dos, o tres, o seguramente ninguna.

Ninguna: 65.43%
Una pieza: 30.78%
Dos piezas: 3.68%
Trez piezas: 0.11%

Probabilidades condicionadas

Hasta ahora vimos las chances de tener flor, y las de tener piezas. Algo que podríamos hacer es ver la probabilidad de estos eventos condicionados entre sí. Es decir, cambiar las preguntas a: ¿Qué tan probable es que tenga pieza dado que tiene Flor? o ¿Qué chances hay de que tenga flor si tengo una pieza? A la primera pregunta se la suele anotar P( Pieza | Flor ), mientras que a la segundase le anota P( Flor | Pieza). Entonces, aclarado este concepto, respondamos las preguntas en el mismo orden que las planteamos.

Sin Flor

Ninguna: 72.71%
Una pieza: 27.29%

Con Flor

Ninguna: 25.61%
Una pieza: 49.86%
Dos piezas: 23.80%
Trez piezas: 0.73%

Notar como cuando tenes flor, aumentan las chances de tener piezas respecto a las chances generales que habíamos visto antes, mientras que cuando no tenemos, suben las chances de no tener piezas. Es importante ver que se cumple:

P( 0 Piezas | No Flor )+P( 1 Pieza | No Flor )=100%

y también:

 P( 0 Piezas | Flor )+P( 1 Pieza | Flor )+P( 2 Piezas | Flor )+P( 3 Piezas | Flor )=100%

Es decir que si sumamos las chances de todos los eventos posibles, dado el condicionamiento, obtenemos la completitud, lo cual tiene sentido.

Ahora respondamos la otra pregunta, que es invirtiendo el orden de lo que acabamos de analizar.

Sin piezas

Sin Flor: 93.93%
Con Flor: 6.07%

Una pieza

Sin Flor: 75.01%
Con Flor: 24.99%

Omitimos los casos de 2 y 3 piezas, pues en esos casos siempre se tiene flor.

Si bien hacer simulaciones no nos cuesta más que unos segundos, podríamos llegar a ahorrarnos algunas simulaciones a partir de usar las probabilidades ya disponibles para calcular nuevas. Para eso resulta muy útil la famosa fórmula de Bayes, la cual nos dice:

P( A | B ) = P( B | A) x P(A) / P(B)

Como vemos nos permite dar vuelta las condicionales. En nuestro caso la podríamos haber usado para ahorrarnos la última simulación. Por ejemplo, veamos cómo a partir de la simulación llegamos a queP( Flor | 1 Pieza)≈25%, pero podríamos haber llegado a lo mismo usando Bayes de la siguiente manera:

P( Flor | 1 Pieza ) = P( 1 Pieza | Flor ) x P( Flor ) / P( 1 Pieza)

Y todos estos valores ya los calculamos anteriormente, pues el primer término fue unos de los primeros condicionales, y los últimos dos surgen de las probabilidades generales que calculamos al principio

P( Flor | 1 Pieza ) = 49.86% x 15.46% / 30.78%  ≈ 25%

Entonces vemos que no es necesario obtener experimentalmente las dos condicionales, si no que basta con obtener una de ellas, y luego apoyarse de las probabilidades generales para obtener la otra.

¿Que chances de ganar el envido tengo?

Dejando atrás el apartado matemático, y con la promesa de no volver a profundizar en esas cuestiones, sigamos nuestro análisis. Veamos ahora cuáles son los puntos de envido más probables, para eso veamos la siguiente gráfica.

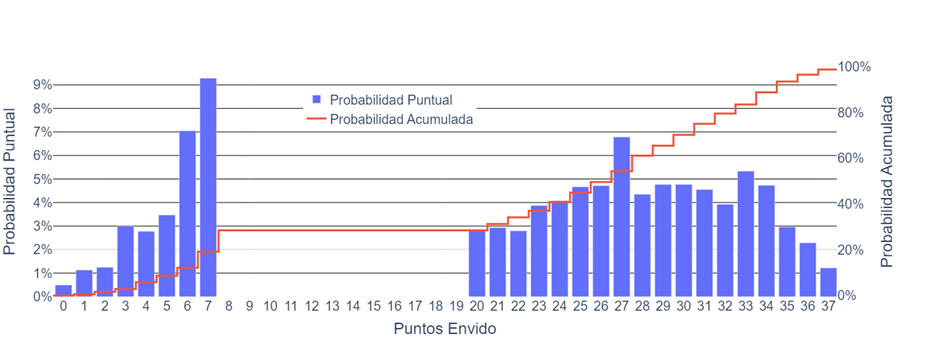
En la gráfica vemos en azúl la probabilidad de obtener determinado puntaje, mientras que en rojo vemos la probabilidad de tener un valor menor al mismo (lo que se denomina acumulado, y lo podemos usar para estimar que chances de ganar tenemos).

De esta figura vemos cosas interesantes; como que es menos probable tener 0 puntos (el mínimo) que 37 (el máximo); que el puntaje más probable es 7 puntos, seguido de 6; o que teniendo más de 20, el puntaje más probable es 27, seguido de 33.

Del  acumulado vemos otras cosas, como que la mitad de los envidos son menores a 26, o que solo un 10% de los envidos son menores a 6 puntos.

¿Y si se que mi rival tiene una pieza?

Acabamos de calcular las probabilidad del envido, igual que como hicimos antes, podemos condicionarlas a tener o no tener pieza. Sin más introducción, veamos los resultados de las simulaciones.

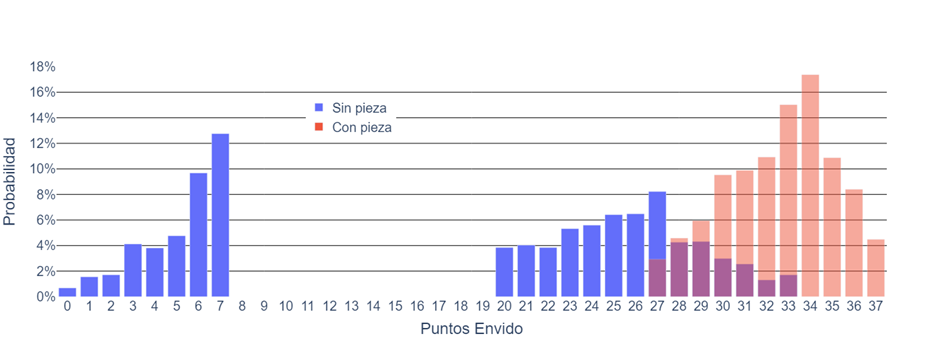
Primero chequeamos lo que esperábamos, y es que si no tenemos pieza los puntos están topeados en 33, mientras que con una pieza, tienen piso en 27. (No analizamos con más de una pieza porque es dicho caso tendríamos flor y corresponde otro análisis)

Otras cosas que podemos ver es que, por ejemplo, si tenemos una pieza, el puntaje más probable es 34, y sin pieza, es 7, igual que en el caso general.

¿Tendrá o no tendrá pieza?

Si el rival tiene entre 27 y 33 de envido, podría o no tener pieza. Esta pregunta que no hacemos es básicamente dar vuelta el condicional, y preguntarnos, dado el puntaje, ¿que chances hay de que tenga una pieza?

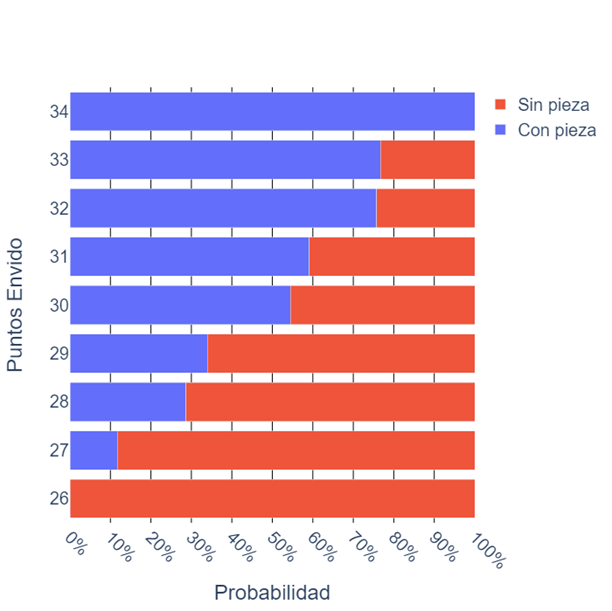
Ahora podemos sacar otras conclusiones, por ejemplo; que si tiene 27, solo hay 11.74% de chances de que tenga pieza; o que si tiene 33, hay una probabilidad mayor al 75% de que tenga pieza.

Lo mismo pero con las flores

Igual que como hicimos para los puntos de envido, podemos repetir exactamente para los puntos de las flores, como se muestra a continuación.

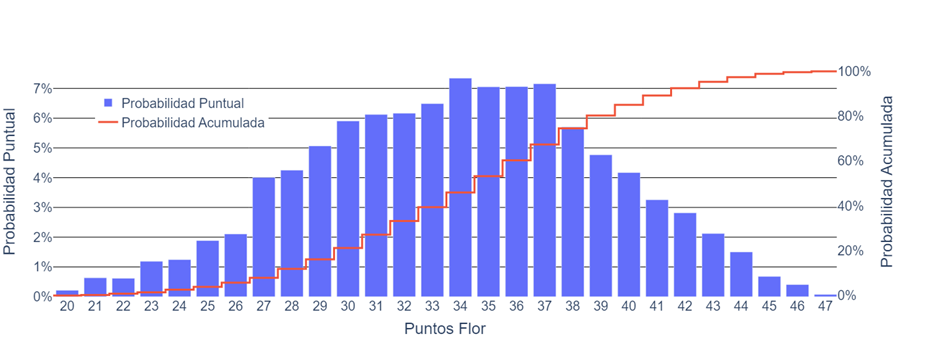
Con los puntajes de las flores tenemos un comportamiento más homogéneo, no habiendo un valor particularmente más probable que el resto, y con valores altos tan probables como valores bajos. Pero si hay que sacar alguna conclusión, es que la mitad de las flores tienen menos de 35 puntos.

Ahora segmentando flores por cantidad de piezas

Podemos nuevamente, condicionar las distribuciones de los puntos de las flores, en base a la cantidad de piezas. Ahora resulta más interesante porque una flor puede tener desde ninguna a 3 piezas, y cada alternativa tiene su propia distribución de puntos, como vemos en la siguiente gráfica.

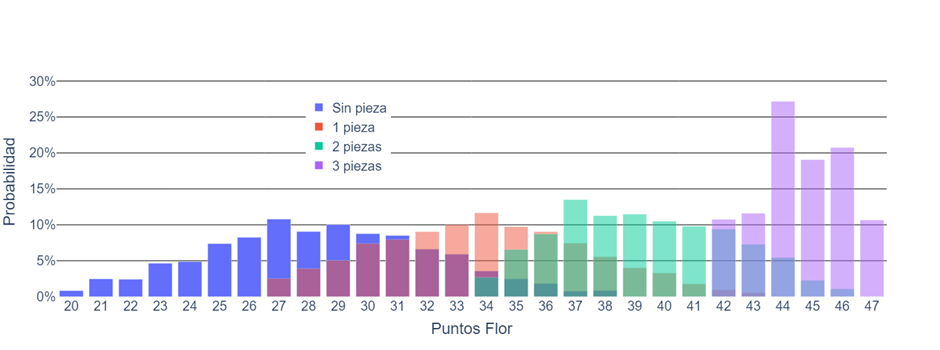
Vemos ahora como; al no tener piezas, el valor más probable es 27 puntos; con una pieza, 34 puntos; con 2 piezas, 37 y con 3 piezas, 44. También vemos como cuantas menos piezas tengamos, más amplio y pobre es el conjunto de valores posibles de nuestra flor.

¿Cuántas piezas tendrá?

Como vimos anteriormente, hay valores de flores para los cuales conviven la posibilidad de tener desde ninguna a 2 piezas, o desde 1 a 3 piezas. Por lo que da juego a hacer nuevamente el análisis inverso, y es obtener las probabilidades de tener determinada cantidad de piezas, en función del valor de la flor.

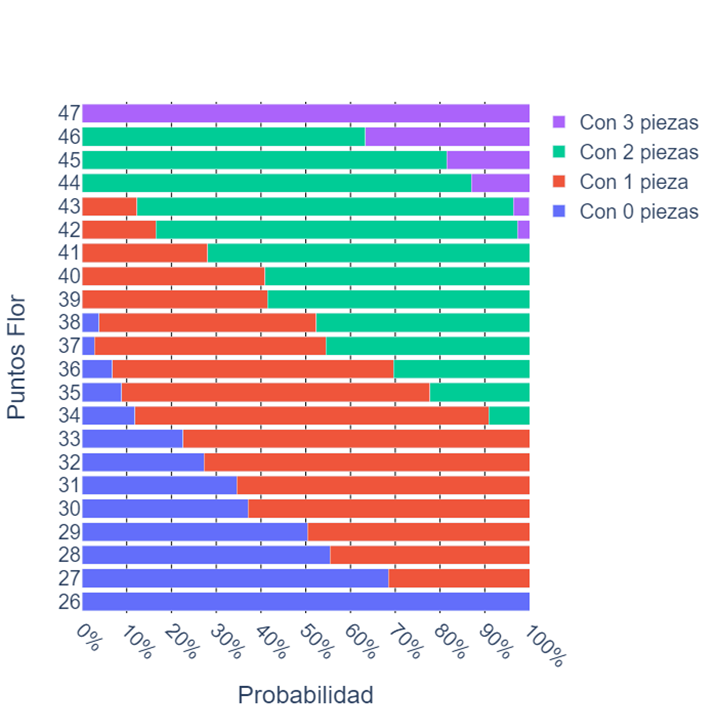
Lo que acabamos de comentar se muestra en la gráfica, y es como, por ejemplo, si la flor es de 42 puntos, bien podría tener 1 pieza (poco probable), 2 piezas (que sería lo más probable) o incluso 3 piezas (lo cual sería bastante extraño pero no imposible).

También nos sirve para asegurarnos cosas, como que si tiene menos de 27, seguro no tiene pieza, o que si tiene más de 38, seguro tenga 2 o más piezas.

Conclusiones, lo que faltó y alguna mentira

A lo largo del blog pudimos confirmar lo útil que son las simulaciones para calcular probabilidades en este tipo de juegos, en donde hay muchas variables a considerar, lo cual dificulta el cálculo exacto por conteo, o al menos, a mi criterio, lo hace inabarcable. Se intentó usar esta herramienta para responder las principales dudas que todos los que jugamos al truco tuvimos alguna vez, aunque es obvio que hay cosas que quedaron fuera del alcance de este análisis.

Algo que no analizamos, para no extender demasiado, es que pasa cuando analizamos a varios jugadores a la vez. Durante todo el blog siempre analizamos qué chances hay de que YO tenga tal cosa, o que YO tenga tal cosa, dado que YO tengo tal otra. Por lo que un futuro análisis podría ser que pasa cuando vemos varios jugadores a la vez y los condicionamos entre sí, individualmente o como equipos.

Por ejemplo, ya respondimos que chance hay de que un jugador tenga flor, pero podríamos preguntarnos ¿Qué chances hay de que jugando uno contra uno, alguno tenga flor? ¿Y jugando dos contra dos, o tres contra tres?. O también ¿Qué chances hay de que jugando dos contra dos haya una flor cruzada? ¿Que tan raro sería que los cuatro tuviésemos flor a la vez? Entre otras tantas preguntas.

Para cerrar y para reforzar la necesidad de un análisis considerando más participantes jugando a la vez, veamos algo que dijimos en el blog y no era tan cierto.

En un momento, cuando hablamos de los puntajes del envido, dijimos que podíamos usar el acumulado para calcular las chances de ganar que teníamos. Sin embargo esto no es tan cierto, pues para que sea cierto se debería cumplir que la mano de mi rival sea independiente de la mía. Y esto claramente no es cierto, porque por ejemplo, si yo tengo 37 de envido, es evidente que mi rival no puede tener 37, porque el 2 de la muestra ya lo tengo yo; o en general, si yo tengo una pieza, es menos probable que mi rival tenga una.

Para valores altos de mi envido, es un error suponer que los puntos de mi rival son independientes a los míos, aunque para valores intermedios es una buena aproximación, y por eso la dejamos en el análisis.