
Más cosas que siempre quisiste saber del Truco Uruguayo (Ahora de a varios)
Haciendo memoria
En la edición anterior de este blog nos centramos en hacer diversos análisis probabilísticos del popular juego de mesa rioplatense (que en realidad vimos que está mucho más extendido de lo que pensamos). Todos estos análisis los hicimos mediante simulaciones, obteniendo las probabilidades buscadas a partir de ver los resultados de millones de simulaciones. De paso aprovechamos para introducir algunos conceptos de la teoría de la probabilidad, como la probabilidad condicional. Además enunciamos y validamos experimentalmente uno de los teoremas más relevantes de la probabilística (y quizás del mundo matemático en general), que fue el teorema de Bayes, viendo su valioso uso para ahorrarnos tiempo en simulaciones que no eran necesarias.
No se juega solo
Todo el análisis que ya hicimos, lo enfocamos en analizar una sola mano, es decir, un solo jugador, aislándonos del resto. Sin embargo, en el truco, como en cualquier otro juego, conocer información del resto de jugadores es vital para desarrollar una estrategia. Además, el truco se puede jugar en diversas modalidades, desde uno contra uno, dos contra dos o tres contra tres. En cada una de estas variantes las dinámicas del juego son distintas, pues cada vez tenemos más cartas sobre la mesa. Es por eso que durante este segundo blog vamos a hacer un análisis orientado a la mesa en general, y no solo a un jugador.
¿Qué tan raro es una flor cruzada?
Para empezar, vamos a ver cual es la probabilidad de que haya una determinada cantidad de flores en una vuelta. Para esto simplemente simulamos como antes, pero ahora en cada iteración generamos tantas manos como jugadores haya jugando.
Caso 1 contra 1
Ninguna: 71.14%
Una flor: 26.67%
Dos flores: 1.19%
En principio los resultados son los esperados, lo más probable es que no haya flor, y que haya una flor cruzada es bastante raro. Ahora veamos algo interesante, la probabilidad de que haya una flor cruzada la podemos ver como:
P(J1 tenga flor Y J2 tenga flor)
Si suponemos que ambos eventos son independientes, entonces la expresión anterior se puede calcular como:
P(J1 tenga flor) x P(J2 tenga flor) = P(Flor)^2
Si recordamos el blog anterior, esta probabilidad es 15.46%, por lo tanto, obtenemos como resultado final 2.39%.
Pero este resultado es casi el doble del obtenido experimentalmente. El error en nuestra cuenta fue pensar que ambos eventos eran independientes, lo cual no es cierto, pues que un jugador tenga flor, reduce las probabilidades de que el otro tenga. El cálculo correcto hubiese sido:
P(J1 tenga flor Y J2 tenga flor) = P(J1 tenga flor) x P(J2 tenga flor | J1 tiene flor) De acá se puede despejar y ver como P(J2 tenga flor | J1 tiene flor) ≈ 7,0%. Es decir que el hecho de que un jugador tenga flor, reduce a más de la mitad las chances de que el otro también tenga.
Caso 2 contra 2
Ninguna: 49.85%
Una flor: 39.19% Tres flores: 1.00%
Dos flores: 9.92% Cuatro flores: 0.03%
Al menos una: 50.15%
Como vemos, a medida que aumenta la cantidad de jugadores, aumentan las chances de que haya una flor en la mesa. En este caso, es casi igual de probable que haya una flor a que no, o sea que en promedio, de cada dos partidas, en una alguien va a cantar.
Caso 3 contra 3
Ninguna: 42.65%
Una flor: 34.42% Cuatro flores: 0.40%
Dos flores: 18.67% Cinco flores: 0.018%
Tres flores: 3.83% Seis flores: 0.0003%
Al menos una: 57.35%
Ya ahora vemos como jugando 3 contra 3, es más probable que haya flor a que no. Esto se debe a la gran cantidad de cartas que hay sobre la mesa.
Vimos entonces cómo a medida que aumentamos la cantidad de jugadores, que ampliamos el alcance de nuestro análisis, cada vez se hace más probable que aparezcan flores en la mesa. A modo de resumen podemos armar la siguiente tabla, para ver como lo que era un suceso poco probable (tener flor), se vuelve cada vez más normal a medida que aumentamos la cantidad de jugadores.
Que un jugador específico tenga flor: 15.46%
Que un 1 contra 1 alguien tenga flor: 26.67%
Que un 2 contra 2 alguno tenga flor: 50.15%
Que un 3 contra 3 alguien tenga flor: 57.35%
¿Y que solo mi equipo tenga flores?
Lo que hicimos recién, era para analizar la cantidad de flores en la mesa, olvidándonos que existen equipos. Es interesante añadir esto al análisis, pues, no es lo mismo que haya 2 flores en la mesa, a que mi equipo sea el que tiene las dos flores; siendo lo segundo menos frecuente que lo primero.
Estos resultados los podríamos calcular a partir de los anteriores. Supongamos que queremos saber qué tan probable es que, jugando 2 contra 2, mi equipo tenga dos flores, y el otro no tenga ninguna. Para calcular eso, partimos de que la chance de que hayan dos flores es 9.92%. Estas dos flores las tienen dos jugadores, de cuatro. Entonces lo único que tendríamos que calcular es que tan probable es que esos dos jugadores, sean los dos de mi equipo. La cantidad de combinaciones de cuatro jugadores, tomados de a 2, son 6, y solo nos sirve una de esas combinaciones, que es la de mi equipo. Entonces la probabilidad que busco es 9.92 / 6 ≈ 1.65%.
De manera similar se pueden calcular el resto de combinaciones, o en nuestro caso, ahorrarnos la parte de combinatoria y simplemente analizar las simulaciones teniendo en cuenta equipos.
Caso 1 contra 1
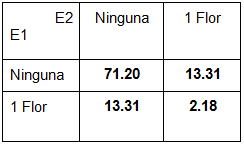
Caso 2 contra 2
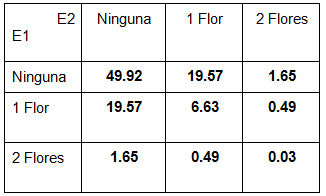
Caso 3 contra 3
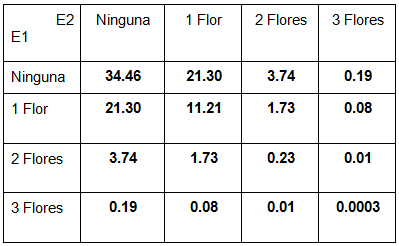
En las tablas vemos lo que ya habíamos comentado, y es que no es lo mismo que haya determinada cantidad de flores en la mesa, a que un equipo tenga esa cantidad. También notamos que todas las tablas son simétricas, lo cual tiene sentido porque no hay distinción entre equipos a la hora de dar las cartas.
¿Y con las piezas pasa lo mismo?
Ya habiendo hecho todo lo que hicimos para las flores, uno podría preguntarse si hay un comportamiento similar con las piezas. En principio uno esperaría un comportamiento similar, y es que a más jugadores, más chances de que aparezcan piezas en la mesa.Pero a diferencia de las flores, las piezas son limitadas, pues son solo 5, mientras que las flores se pueden armar de diversas maneras. Aunque es innegable que hay una alta correlación entre la cantidad de piezas en mesa y la cantidad de flores cantadas.
Repitamos el mismo análisis de antes pero ahora con piezas.
Caso 1 contra 1
Ninguna: 41.24%
Una pieza: 42.67%
Dos piezas: 14.17%
Tres piezas: 1.83%
Cuatro piezas: 0.08%
Cinco piezas: 0.001%
Caso 2 contra 2
Ninguna: 14.07%
Una pieza: 36.54%
Dos piezas: 33.51%
Tres piezas: 13.42%
Cuatro piezas: 2.32%
Cinco piezas: 0.13%
Caso 3 contra 3
Ninguna: 3.54%
Una pieza: 18.72%
Dos piezas: 35.32%
Tres piezas: 29.75%
Cuatro piezas: 11.19%
Cinco piezas: 1.48%
Con estos datos confirmamos lo que pensábamos, y es que a medida que hay más jugadores, menos probable es que no haya piezas de por medio. Llegando al caso extremo de 3 contra 3, donde es muy raro que no haya ni una sola pieza.
¿Es raro que mi equipo tenga todas las piezas?
Nuevamente podemos repetir el análisis pero considerando los equipos, para ver cómo tienden a distribuirse las piezas entre los equipos.
Caso 1 contra 1
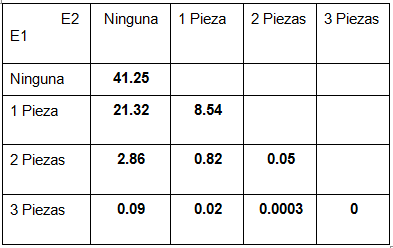
Caso 2 contra 2
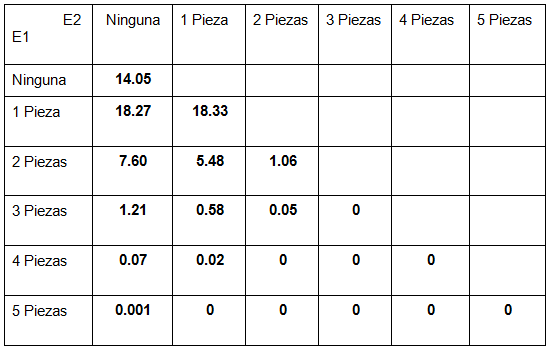
Caso 3 contra 3
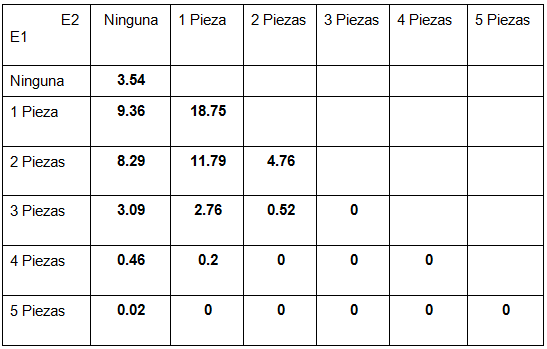
Cosas a notar en estas tablas es que; como ya vimos que son simétricas, ignoramos los valores del triángulo superior para no sobrecargar; además que ahora aparecen valores en 0, y es que hay combinaciones que superan las 5 piezas, las cuales obviamente son imposibles.
¿Y qué pasa con los envidos?
¿Se podría hacer el mismo análisis con los puntos de Envido? Si ¿Lo vamos a hacer? No ¿Porque? Como se explicó en el blog anterior, los puntos de envido no son tan sensibles a los condicionamientos de los demás jugadores, salvo que tengamos puntajes muy altos, momento en el cual si empiezan a aparecer ligeros efectos de condicionamiento. Es por esto que no vale la pena analizar los puntos de envido desde la misma perspectiva que estábamos haciendo con flores y piezas.
Lo que si vamos a hacer es, pasar de las probabilidades de tener determinado envido, que calculamos en el blog pasado, a que la pareja tenga determinado puntaje. El puntaje de la pareja es simplemente el máximo del puntaje de ambos, esto se puede expresar como:
max ( {P1 , P2} )
Si nuevamente hacemos la suposición equivocada de que ambas variables son independientes (aunque ahora no es tan inverosímil), lo que querríamos calcular es la distribución del máximo de una misma distribución muestreada dos veces, a partir de la distribución original. A este concepto en estadística se lo conoce como el estadístico de orden 2 (análogamente lo que querríamos sería el estadístico de orden 3 si se jugasemos de a 6)
Usualmente es bastante complicado calcular los estadísticos de distinto orden a partir de la distribución original. Sin embargo para nosotros va a ser muy fácil pues alcanza con tomar el máximo de los distintos envidos simulados y analizar esa distribución.
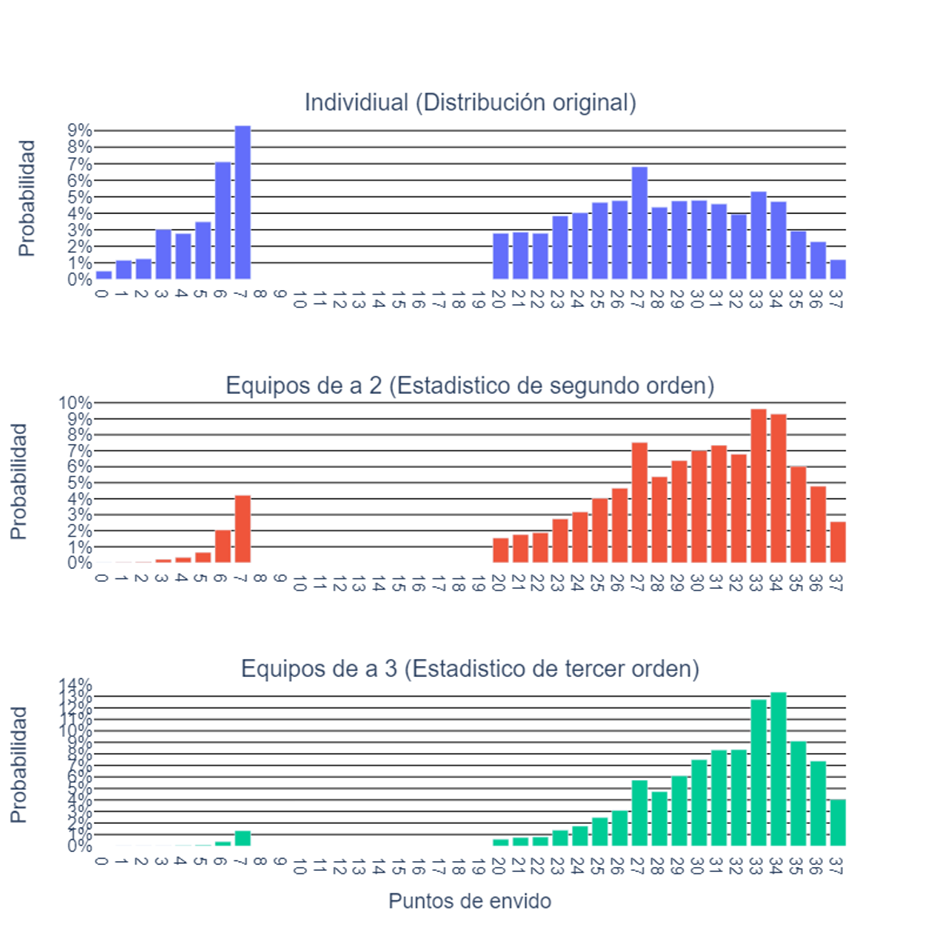
Vemos entonces, cómo a medida que aumenta la cantidad de jugadores por equipo, más probable es obtener puntajes altos, lo cual tiene sentido pues el puntaje del equipo es el máximo del de sus integrantes. Por ejemplo, cuando analizamos a un jugador por separado, es bastante probable tener puntajes por debajo de los 20, sin embargo, cuando jugamos de a 6, es casi imposible que un equipo obtenga esos puntajes.
Si en vez de analizar solo los puntajes de un equipo, analizamos las distribuciones de los puntajes máximos de la mesa, es decir, considerando 4 manos (2 contra 2) o 6 manos (3 contra 3), podemos obtener estadísticos de mayor orden a los ya mostrados.
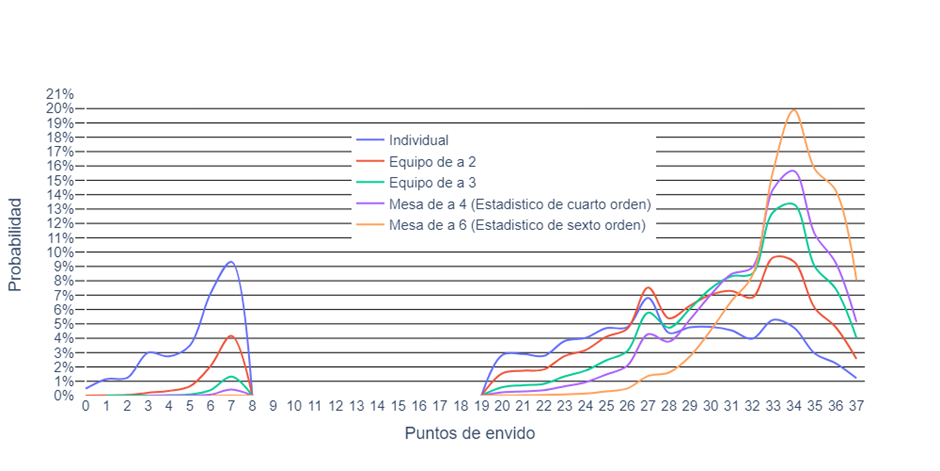
Ahora ya con más estadísticos en juego, es fácil ver cómo a medida que sube el orden de los mismos, tienden a inclinarse cada vez más hacia la derecha, hacia los tantos más altos.
Una acotación necesaria es que si bien era una buena aproximación considerar los tantos de cada jugador como independientes cuando veíamos solo a una pareja, al momento de considerar una mesa entera de 6 jugadores, es probable que nuestra suposición ya no sea tan verosímil y realmente lo que estamos viendo difiere bastante del estadístico real.
Por último veamos las distribuciones acumuladas en cada una de estas situaciones.
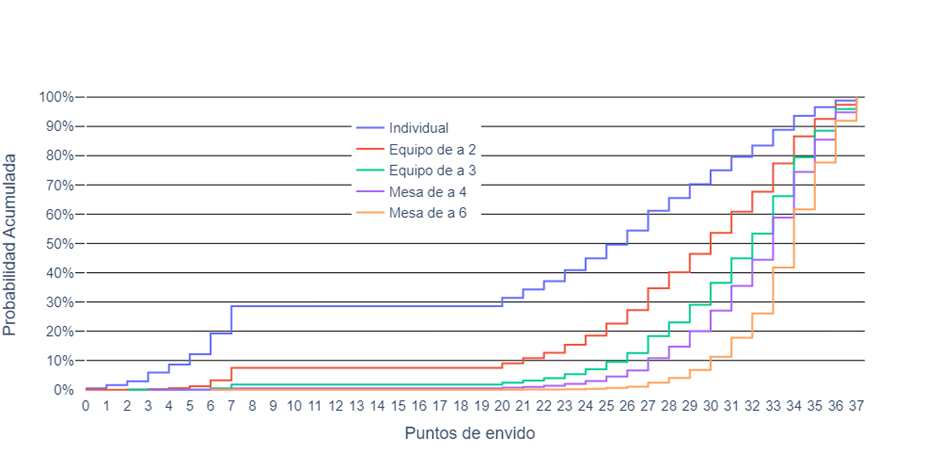
Está gráfica nos permite ver cosas interesantes, por ejemplo, si vemos el umbral de 50% de probabilidad acumulada, estamos viendo cuál es la mediana de la distribución, es decir, aquel valor sobre el cual estarán la mitad de los tantos, mientras que la otra mitad estará por debajo. Entonces podemos ver como cuando analizamos a un jugador por separado, la mitad de los envidos serán superiores a 25; cuando vemos a una pareja, a 30; cuando veamos a un trío, a 32; cuando veamos una mesa de a 4, a 33 y finalmente cuando vemos una mesa de a 6, la mitad de los envidos van a tener un puntaje superior a los 34 puntos.
Podríamos también, en vez de fijar una probabilidad acumulada y determinar valores, fijar un valor y ver qué probabilidad acumulada tiene ese puntaje para cada situación. Por poner un ejemplo, veamos qué pasa con los 30 puntos. Cuando analizamos individualmente, solo un cuarto de las veces los envidos son mayores a dicho valor; cuando veamos a una pareja, el 47% de las veces; cuando veamos a un trío, el 63% de las veces; cuando vemos una mesa entera de a 4, el 73% de las veces y finalmente cuando vemos el caso más extremo, una mesa de a 6, casi el 90% los envidos superarán dicho puntaje.
Conclusiones
En esta segunda parte profundizamos en el condicionamiento entre jugadores, que realmente es la base de este tipo de juegos, donde es tan valioso tener información del rival. Analizamos también cómo se relaciona el comportamiento estadístico de un jugador, en comparación al del equipo, y cómo este varía dependiendo de la cantidad de jugadores que haya en el equipo. Introducimos nuevos conceptos estadísticos un poco más complejos, como fueron los ordenes estadísticos, viendo justamente como relacionaban el comportamiento individual con el colectivo. También analizamos los errores que puede traer considerar como independientes sucesos que en realidad no lo son, o como a veces, podemos tomar un concepto más laxo de independencia en pos de simplificar los razonamientos.
