
Analizando series temporales a partir de la música
¿Qué es y cómo se ve una nota musical? ¿Y un acorde?
En este post vamos a tratar de introducir un concepto muy importante y muy útil en el procesamiento de cualquier cosa interpretable como una serie temporal, que es la representación frecuencial. Pero para abordar el tema de una forma más amigable e intuitiva, vamos a ver como se aplicaría la herramienta en el caso de una onda de sonido, y como nos ayuda a interpretarla musicalmente.
Antes de introducirnos en que es la representación en frecuencia, veamos algunos conceptos importantes para entender bien que es una onda sonora y que cosas son interesantes extraer de ella en un contexto musical y como se manifiestan las mismas.
¿Cómo se genera el sonido?: La mayoría de los instrumentos musicales producen su sonido haciendo vibrar el aire, de alguna u otra manera. Por ejemplo, una guitarra (o en general los de cuerda) hace vibrar al aire justamente haciendo vibrar sus cuerdas, o una trompeta (y la mayoría de vientos) haciendo vibrar el aire en su interior, incluso los instrumentos de percusión también, haciendo vibrar su membrana.
¿Pero qué significa hacer vibrar el aire?: Cuando hablamos de hacer vibrar al aire, nos referimos a provocar pequeñas variaciones (oscilaciones) en la presión del mismo, algo así como comprimir y expandir al aire muy rápido. Así que cuando hablamos de sonido, hablamos de una onda que es capaz de propagarse por al aire a través de estas oscilaciones, las cuales finalmente puede captar nuestro oído detectando estos cambios de presión.
Ahora estamos en condiciones de entender que es una nota musical. Cuando hablamos de que el sonido no es más que la vibración del aire, hay que entender que esta oscilación puede ser más o menos rápida (más aguda o más grave). En función a que tan rápida se de esta oscilación (ciclos de compresión y descompresión del aire por segundo) podemos clasificar estos sonidos, dando así lugar a las notas musicales.
Por ejemplo, el estándar indica que si el aire vibra 440 veces por segundo (lo que se escribe como 440Hz), decimos que ese sonido corresponde a la nota “La”. En base a este estándar se puede inferir el resto de las 12 notas musicales de la escala cromática.
Es importante saber que debido a las leyes físicas y matemáticas que gobiernan las vibraciones del aire (y que de momento no vamos a ahondar), las notas son cíclicas. Es decir, si bien dijimos que el “La” corresponde a 440Hz, toda otra frecuencia obtenida a partir de multiplicar o dividir por 2 a la misma, resultará en la misma nota. O sea, 110Hz, 220Hz, 440Hz, 880Hz y 1760Hz son todos “La”, todos consonantes entre sí, aunque cada uno más agudo que el otro.
Algunos conceptos que es importante introducir ahora que entendimos el concepto de frecuencia:
Distancia de octava: A la cantidad de veces que tenemos que multiplicar o dividir por dos para llegar de una nota a otra versión de la misma, la llamamos distancia en octavas. Por ejemplo, para ir del “La” de 110Hz, tenemos que multiplicar 3 veces por dos, para llegar al “La” de 880Hz, decimos que esos dos “La” están a una distancia de 3 octavas.
Distancia entre notas: Dada la frecuencia de una nota, se puede obtener la de la siguiente, multiplicando por raíz duodécima de dos (~1.05946), o la anterior, dividiendo por el mismo número. Por ejemplo, dado el “La” de 440Hz, podemos obtener la siguiente nota “La#” al multiplicar 440Hz por 1.05946, obteniendo así 446Hz. Y podemos repetir el proceso sucesivamente para obtener la frecuencia de todas las notas, teniendo siempre una base de la que partir, en este caso el “La” a 440Hz, que se establece así por convención.
Rango de audición: En el mejor de los casos, un humano es capaz de oír en el rango de frecuencias de 20Hz a 20kHz (20.000Hz). Aunque este rango va disminuyendo drásticamente con la edad.
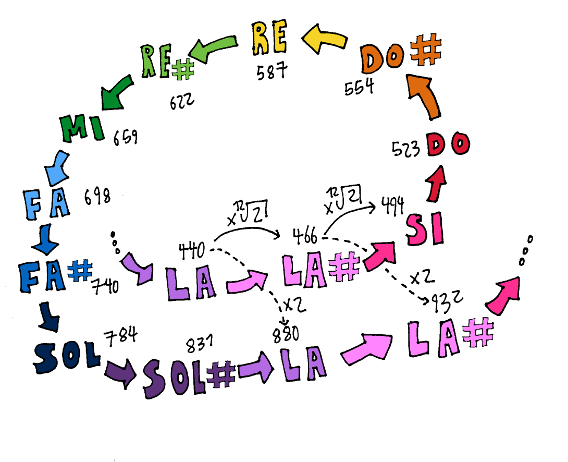
Dicho esto, resulta muy fácil explicar que es un acorde, ya que simplemente es cualquier combinación de 3 o más notas distintas, tocadas simultáneamente. Un detalle a notar es que no todos los instrumentos tienen la capacidad de tocar varias notas a la vez, por lo tanto, no todos los instrumentos son capaces de tocar acordes por si solos. Los que si pueden tocar distintas notas a la vez son llamados polifónicos (guitarra, piano) y los que no, monofónicos (trompeta, flauta).
Ahora estamos listos para “ver” las notas, para eso vamos a observar lo que registra un micrófono, que no es más que una forma de digitalizar las ondas de presión que conforman el sonido.
Vamos a observar en primer lugar la nota “Mi” a 330Hz, producida por un piano:
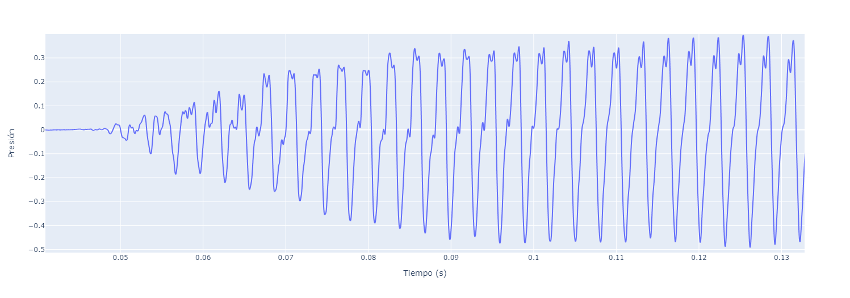
En la gráfica vemos como varía la presión en función del tiempo. Como hablamos antes, podemos ver que efectivamente es una oscilación que se repite, comprimiéndose y descomprimiéndose, subiendo y bajando. En la gráfica vemos el sonido desde el principio, es decir somos capaces de ver el silencio (valor 0 en el eje vertical) y como empieza a vibrar la cuerda del piano generando la onda descrita (¡sí, si no lo sabías, el piano tiene cuerdas!).
Si bien este es el sonido como lo entendemos, es lo que mide un micrófono y lo que interpreta nuestro tímpano, a la vista está grafica no nos aporta mucha información.
Menos aun cuando vemos un acorde, por ejemplo, de “Mi séptima”, que está compuesto ahora por 4 notas (“Mi”, “Sol#”, “Si” y “Re”), tocado en guitarra.
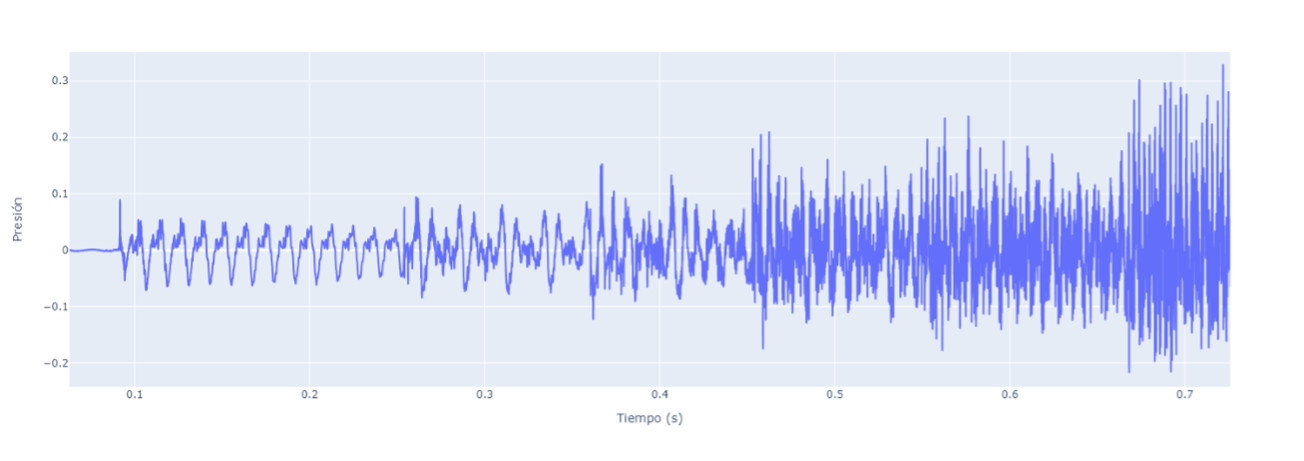
Ahora que hay cuatro oscilaciones a la vez, que empiezan a sonar en tiempos distintos, es mucho más difícil identificar cada una de las notas o siquiera entender que es lo que está pasando.
¿Cómo volver estos datos más visuales, intuitivos e informativos?:
Antes de responder está pregunta, tenemos que entender que lo que estamos viendo en las gráficas superiores, es una representación temporal. Una representación temporal nos informa como varía cierta magnitud (presión en este caso) en función del tiempo. Es la forma más común y sencilla de pensar las cosas, aunque no siempre es la más representativa, como veremos es este caso.
¿Qué otras representaciones existen?:
Existe otra representación muy usada en el mundo del procesamiento de audio (aunque también en otras áreas, como procesamiento de imágenes) que es la representación en frecuencia. Al principio es difícil de entender el concepto, pero una vez se entiende resulta extremadamente útil para pensar y abordar problemas, como por ejemplo, el interpretar estos datos que estamos trabajando.
La representación frecuencial consiste ya no en informar como varía la magnitud medida en función del tiempo, si no, en cómo está compuesta la totalidad de la señal, en base a las frecuencias que hay en ella. O con una visión más técnica, como se distribuye la energía de la señal en función de la frecuencia.
En resumen, mientras en una representación temporal, podemos ver en un determinado tiempo, la magnitud medida; en una representación frecuencial vemos, dada una determinada frecuencia, que tan presente está en la señal registrada.
La herramienta matemática concreta que nos permite obtener la representación frecuencial en base a la temporal (y viceversa) es la denominada «Transformada de Fourier», la cual está implementada en casi cualquier lenguaje de programación.
Viendo una nota: Como anticipamos antes, el mejor escenario para aplicar esto, es cuando trabajamos con señales de audio como estábamos haciendo. Así que veamos ahora la representación frecuencial de la misma nota “Mi”.
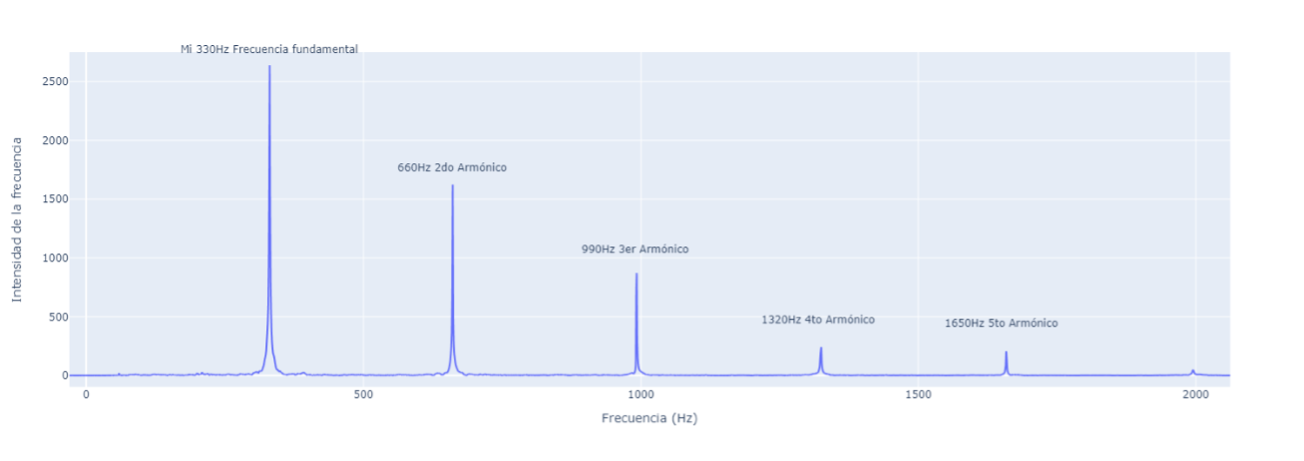
Y esto, es una representación en frecuencia. Vamos a ir viendo la nueva grafica para identificar los elementos y asociarlos con los conceptos desarrollados previamente.
En primer lugar, veamos que la “intensidad de la frecuencia” es nula en todas las frecuencias menos en ciertos valores puntuales, donde toma valores bastante altos. El primer pico que observamos está en 330Hz ¡Que justamente es la frecuencia del “Mi”!
Y tiene todo el sentido del mundo, porque justamente un “Mi” es una oscilación con frecuencia 330Hz, por lo tanto, es lógico que sea la frecuencia más presente en la señal, por no decir la única.
Ahora, no todo es felicidad, ¿Por qué aparecen picos en otros valores? ¿Qué sentido tienen?
Bueno, lo primero que hay que notar es que estos otros picos no están en cualquier frecuencia, están en múltiplos de 330Hz. Se llaman “armónicos”, y aparecerán siempre en múltiplos de la frecuencia de la vibración (frecuencia fundamental), a no ser, que esta vibración sea lo que llamaremos “oscilación pura”, donde en dicho caso solo aparecería un pico en la frecuencia fundamental.
Explicar que es una “oscilación pura” y explicar realmente que son los “armónicos”, es algo que excede el objetivo de este post y nos meteríamos en terrenos mucho más pantanosos. Lo único que me gustaría dejar picando, es que los armónicos son los causantes de la naturaleza cíclica de las notas, que mencionamos al principio del artículo.
Viendo un acorde: Ahora con los conceptos más o menos aclarados para el caso de una nota aislada, estamos listos para usar esta representación sobre un acorde, que es donde muestra su verdadero potencial.
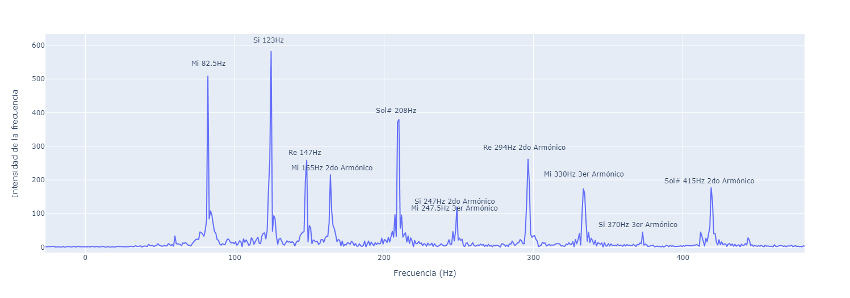
Recordemos ahora que lo que estamos viendo es la representación frecuencial del acorde de “Mi séptima” compuesto por las notas “Mi”, “Sol#”, “Si” y “Re”. Entonces podemos ver en la gráfica como todas estas cuatro notas aparecen como picos en sus respectivas frecuencias, al igual que lo hacen también sus armónicos en los múltiplos de las mismas. (Que los picos de cada nota tengan altura distinta, está asociada al concepto de “distorsión armónica”)
Y así es como pudimos pasar de una representación temporal del acorde, que poco y nada aportaba a su interpretación, a una de frecuencia, donde podemos distinguir claramente que frecuencias lo componen, identificando así las notas del mismo. Y es importante notar que en ningún momento nos tuvimos que preocupar porque las notas no empezasen a sonar a la misma vez, ya que está es una de las principales fortalezas de la representación frecuencial, separar completamente el tiempo de la ecuación, centrándonos únicamente en su composición frecuencial, sin importar el orden temporal (es verdad que, una de las desventajas de esta representación, es que perdemos la noción temporal, por lo tanto, el orden).
Como corolario vale agregar que, si bien nosotros pasamos de la representación temporal a la frecuencial, se puede hacer al revés. Esto da juego a muchas ideas para modificar el sonido, modificándolo en frecuencia para luego llevarlo al tiempo y obtener el sonido original con nuevas características, tema que seguramente tratemos en otro post.
Aplicaciones directas: Todos estos conceptos aprendidos sobre el análisis en frecuencia tienen muchísimas aplicaciones en otras áreas y sectores comerciales, de las cuales detallaremos un par a continuación.
Detección de frecuencia cardíaca: Una aplicación bastante directa es la detección de la frecuencia cardíaca a partir de un electrocardiograma. Un electrocardiograma es una representación de la actividad eléctrica del corazón a lo largo del tiempo, lo cual podemos identificar claramente como una serie temporal. En esta señal se manifiestan las pulsaciones del corazón, las cuales son claramente periódicas. Una de las primeras y más básicas cosas que podemos hacer con esta serie es identificar la frecuencia de las pulsaciones. Para esto podemos aplicar exactamente lo mismo que hicimos con las ondas de sonido para identificar su frecuencia, y de esta manera detectar el ritmo de las pulsaciones.

Análisis de periodicidad: Un caso muy usual es cuando en ciertas medidas a lo largo del tiempo (series temporales), por ejemplo, ventas de una empresa, porcentaje de ganancia, demanda, etc. haya períodos cíclicos que se repiten a lo largo del tiempo. Ya sea el caso de una tienda de artículos de playa, la cual tendrá claramente una tendencia a aumentar sus ventas en verano y a disminuir en invierno; o bien el caso de un local de comida, donde seguramente tenga mayor demanda un fin de semana que cualquier otro día de la semana. En algunos casos es obvio detectar cual es el período de estos ciclos (un año y una semana, respectivamente, en los ejemplos dados), pero en otros no lo es, o simplemente nos interesa automatizar este proceso sin la necesidad de tener a un especialista del rubro que lo identifique. Es acá cuando podemos usar lo visto, para detectar la frecuencia con que se repiten estos ciclos, de la misma manera que detectamos la frecuencia del sonido para detectar cada nota musical. Entonces vemos que nuevamente podemos pasar al dominio de la frecuencia de una serie temporal para identificar y medir características de la misma que sería muy complicado hacerlo directamente en el dominio temporal.

Conclusiones: En general el concepto de la representación en frecuencia puede ser aplicada a cualquier serie temporal para obtener información que de otra manera no sería evidente; y esto nos permite obtener una visión distinta de muchos problemas, permitiéndonos obtener muchas veces soluciones sencillas, robustas e interpretables fácilmente. Realmente se puede decir que la única limitación es la imaginación, puesto que estos conceptos que tratamos, si bien lo hicimos siempre pensándolos sobre series temporales, sobre cosas que medimos a lo largo del tiempo, pueden ser aplicadas a cualquier otro tipo de información numérica que tengamos, por ejemplo, sobre los pixeles de una imagen para hacer procesamiento de imágenes, entre otras tantas cosas.
